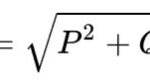インダクタンスは、磁場のエネルギーを蓄積するための電気回路の要素の特性を特徴づけます。また、電流と磁場の関係の尺度でもあります。それはまた、電気の慣性と比較されます-ちょうど機械体の慣性の尺度を持つ質量のように。

コンテンツ
自己誘導の現象
導電回路を流れる電流の大きさが変化すると、自己誘導現象が発生します。この場合、回路を通る磁束が変化し、自己誘導起電力と呼ばれる起電力が電流ループの端子に現れます。このEMFは電流の方向と反対であり、次のようになります。
ε=-ΔF/Δt=-L*(ΔI/Δt)
自己誘導のEMFは、回路を流れる電流の変化によって引き起こされる磁束の変化率に等しく、電流の変化率にも比例することは明らかです。自己誘導のEMFと電流の変化率の間の比例係数はインダクタンスと呼ばれ、Lで表されます。この値は常に正であり、SI単位は1ヘンリー(1 H)です。フラクショナルフラクションも使用されます-ミリヘンリーとマイクロヘンリー。 1アンペアの電流の変化が1ボルトの自己誘導EMFを引き起こす場合、1ヘンリーのインダクタンスについて話すことができます。回路にはインダクタンスがあるだけでなく、直列に接続された回路のセットとして表すことができるコイルだけでなく、別個の導体もあります。
インダクタンスはエネルギーを蓄えます。これはW=L*Iとして計算できます。2/ 2、ここで:
- W-エネルギー、J;
- L –インダクタンス、H;
- Iはコイルの電流Aです。
そしてここで、エネルギーはコイルのインダクタンスに正比例します。
重要! 工学では、インダクタンスは電界が蓄積されるデバイスでもあります。このような定義に最も近い実際の要素はインダクタです。
物理コイルのインダクタンスを計算するための一般式は複雑な形式であり、実際の計算には不便です。インダクタンスは巻数、コイルの直径に比例し、幾何学的形状に依存することを覚えておくと便利です。また、インダクタンスは巻線が配置されているコアの透磁率の影響を受けますが、ターンを流れる電流は影響を受けません。インダクタンスを計算するには、特定の設計について上記の式を参照する必要があるたびに。したがって、円筒形コイルの場合、その主な特性は次の式で計算されます。
L=μ*μ*(N2* S / l)、
どこ:
- μはコイルコアの比透磁率です。
- μ –磁気定数、1.26 * 10-6 H / m;
- Nはターン数です。
- Sはコイルの面積です;
- lはコイルの幾何学的長さです。
円筒形コイルや他の形状のコイルのインダクタンスを計算するには、オンライン計算機などの計算機プログラムを使用することをお勧めします。
インダクタの直列および並列接続
インダクタンスは直列または並列に接続でき、新しい特性を備えたセットを取得します。
並列接続
コイルが並列に接続されている場合、すべての要素の電圧は等しく、電流(変数)は、要素のインダクタンスと逆に分布します。
- U = U1= U2= U3;
- I = I1+ I2+ I3.
回路の総インダクタンスは1/L = 1/Lとして定義されます1+ 1 / L2+ 1 / L3。この式は任意の数の要素に有効であり、2つのコイルの場合はL=Lの形式に簡略化されます。1* L2/(L1+ L2)。明らかに、結果として生じるインダクタンスは、最小値の要素のインダクタンスよりも小さくなります。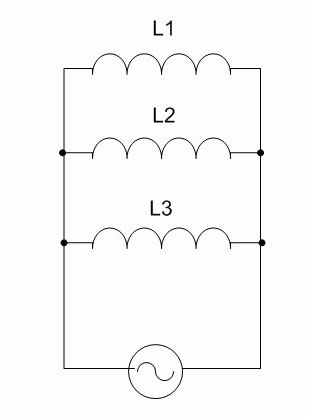
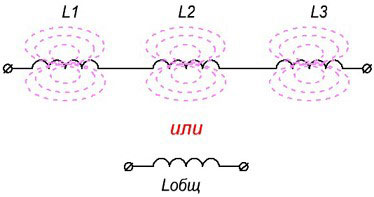
シリアル接続
このタイプの接続では、同じ電流がコイルで構成された回路を流れ、回路の各コンポーネントの電圧(可変!)は、各要素のインダクタンスに比例して分配されます。
- U = U1+ U2+ U3;
- I = I1= I2= I3.
合計インダクタンスはすべてのインダクタンスの合計に等しく、最大値を持つ要素のインダクタンスよりも大きくなります。したがって、このような接続は、インダクタンスを増加させるために必要に応じて使用されます。
重要! 直列または並列のバッテリーでコイルを接続する場合、計算式は、要素の相互の磁場の相互影響を除外した場合(シールド、長距離など)でのみ正しいものです。影響がある場合、インダクタンスの合計値はコイルの相対位置に依存します。
インダクタのいくつかの実用的な問題と設計
実際には、さまざまな設計のインダクタが使用されます。用途や用途に応じてさまざまな方法で作ることができますが、実際のコイルで発生する影響を考慮する必要があります。
インダクタの品質係数
実際のコイルには、インダクタンスに加えて、さらにいくつかのパラメーターがあり、最も重要なものの1つは品質係数です。この値はコイルの損失を決定し、以下に依存します。
- 巻線のオーミック損失(抵抗が大きいほど、品質係数は低くなります)。
- ワイヤ絶縁および巻線フレームの誘電損失。
- 画面の損失;
- コア損失。
これらすべての量が損失抵抗を決定し、品質係数はQ=ωL/Rlossesに等しい無次元値です。ここで、
- ω=2*π*F-角周波数;
- L-インダクタンス;
- ωLはコイルのリアクタンスです。
品質係数は、アクティブに対する反応性(誘導性)抵抗の比率に等しいとほぼ言えます。一方では、周波数が高くなると分子が増加しますが、同時に、表皮効果により、ワイヤの有効断面積が減少するため、損失抵抗も増加します。
スクリーン効果
異物の影響だけでなく、電界と磁界、およびこれらの磁界を介した要素の相互影響を減らすために、コイル(特に高周波のもの)がスクリーンに配置されることがよくあります。有益な効果に加えて、シールドはコイルの品質係数の低下、そのインダクタンスの低下、および寄生容量の増加を引き起こします。さらに、スクリーンの壁がコイルの巻きに近いほど、有害な影響が大きくなります。したがって、シールドコイルはほとんどの場合、パラメータを調整できるように作られています。
トリマーインダクタンス
場合によっては、コイルを他の回路素子に接続した後、現場でインダクタンス値を正確に設定し、チューニング中のパラメータの偏差を補正する必要があります。このために、さまざまな方法(ターンのタップの切り替えなど)が使用されますが、最も正確でスムーズな方法は、コアを使用して調整することです。それは、コイルのインダクタンスを調整して、フレームの内側にねじ込んだり外したりすることができるねじ山の形で作られています。

可変インダクタンス(バリオメーター)
インダクタンスまたは誘導結合の迅速な調整が必要な場合は、異なる設計のコイルが使用されます。それらには、可動と固定の2つの巻線が含まれています。合計インダクタンスは、2つのコイルのインダクタンスとそれらの間の相互インダクタンスの合計に等しくなります。
あるコイルの相対位置を別のコイルに変更することにより、インダクタンスの合計値が調整されます。このような装置はバリオメーターと呼ばれ、何らかの理由で可変コンデンサーの使用が不可能な場合に共振回路を調整するために通信機器でよく使用されます。バリオメーターの設計はかなりかさばり、その範囲が制限されます。

印刷されたスパイラルの形のインダクタンス
インダクタンスの小さいコイルは、印刷された導体のスパイラルの形で作ることができます。この設計の利点は次のとおりです。
- 生産の製造可能性;
- パラメータの高い再現性。
欠点には、調整中の微調整が不可能であり、大きなインダクタンス値を取得することが難しいことが含まれます-インダクタンスが高いほど、コイルがボード上で占めるスペースが大きくなります。

断面巻きリール
静電容量のないインダクタンスは紙にのみあります。コイルを物理的に実装すると、寄生ターン間容量がすぐに発生します。多くの場合、これは有害です。寄生容量はLC回路の容量に加算され、発振システムの共振周波数と品質係数を低下させます。また、コイルには独自の共振周波数があり、望ましくない現象を引き起こします。
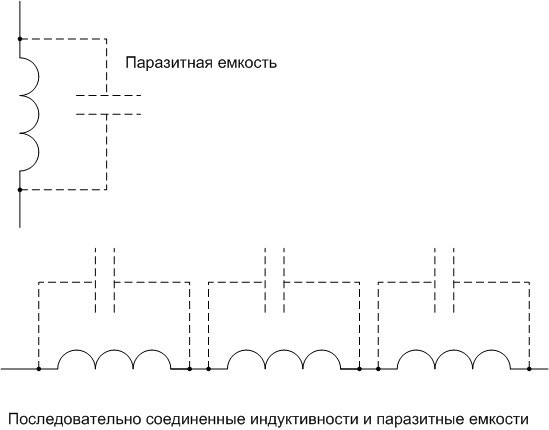
寄生容量を減らすためにさまざまな方法が使用されますが、最も簡単な方法は、いくつかの直列接続されたセクションの形での巻線インダクタンスです。これを含めると、インダクタンスが加算され、総容量が減少します。

トロイダルコア上のインダクタ
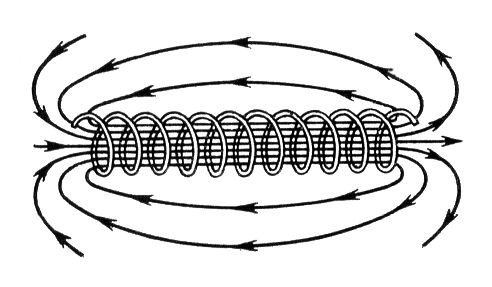
円筒形インダクタの磁力線は、巻線の内側(コアがある場合はそれを通ります)を通り、外側から空気を介して閉じられます。この事実には、いくつかの欠点があります。
- インダクタンスが減少します。
- コイルの特性は計算にあまり適していません。
- 外部磁界に物体を持ち込むと、コイルのパラメータ(インダクタンス、寄生容量、損失など)が変化するため、多くの場合、シールドが必要になります。
トロイダルコア(リングまたはドーナツの形で)に巻かれたコイルには、これらの欠点がほとんどありません。磁力線は閉ループの形でコアの内部を通過します。これは、外部オブジェクトがそのようなコアに巻かれたコイルのパラメータに実質的に影響を及ぼさないことを意味し、そのような設計にはシールドは必要ありません。インダクタンスも増加し、他の条件は同じであり、特性の計算が容易になります。
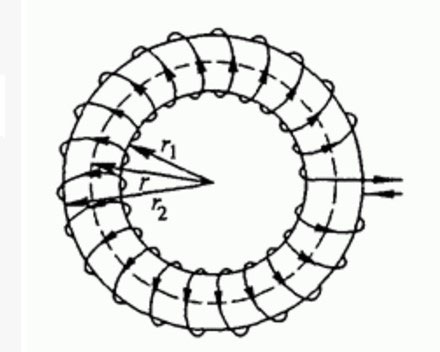
トーラスに巻かれたコイルの欠点は、その場でインダクタンスをスムーズに調整できないことです。もう1つの問題は、巻線の労働強度が高く、製造可能性が低いことです。ただし、これは一般に、多かれ少なかれすべての誘導要素に適用されます。
また、インダクタンスの物理的な実装の一般的な欠点は、重量とサイズが大きく、信頼性が比較的低く、保守性が低いことです。
したがって、技術では、彼らは誘導性成分を取り除こうとします。ただし、これが常に可能であるとは限らないため、巻線コンポーネントは、近い将来と中期の両方で使用されます。
同様の記事: